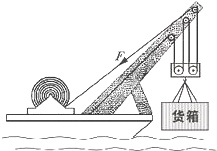
如图是某水上打捞船起吊装置结构示意简图.某次打捞作业中，该船将沉没于水下20米深处的一只密封货箱打捞出水面，已知该货箱体积为50m3，质量是200t. 求：(1)货箱在该深度处受到水的压强是多大?

如图是某水上打捞船起吊装置结构示意简图.某次打捞作业中，该船将沉没于水下20米深处的一只密封货箱打捞出水面，已知该货箱体积为50m3，质量是200t.

求：(1)货箱在该深度处受到水的压强是多大?

(2)货箱完全浸没在水中时受到的浮力是多少?

(3)货箱完全出水后，又被匀速吊起1m，已知此时钢缆拉力F为1×106N，则在此过程中拉力F所做的功是多少?起吊装置的滑轮组机械效率是多少?(水的密度为1.0×103kg/m3，g取10N/kg，)

 

(1) 货箱在水下 20 米处受到的水的压强

公式：

p=ρ水ghp=ρ水​gh

已知：
ρ水=1.0×103 kg/m3ρ水​=1.0×103 kg/m3，
g=10 N/kgg=10 N/kg，
h=20 mh=20 m。

p=1000×10×20=2.0×105 Pap=1000×10×20=2.0×105 Pa

所以：

2.0×105 Pa2.0×105 Pa​

---

(2) 货箱完全浸没时受到的浮力

浮力公式：

F浮=ρ水gV排F浮​=ρ水​gV排​

完全浸没时：

V排=V箱=50 m3V排​=V箱​=50 m3F浮=1000×10×50=5.0×105 NF浮​=1000×10×50=5.0×105 N

所以：

5.0×105 N5.0×105 N​

---

(3) 货箱完全出水后，被匀速吊起 1 m 时的做功与机械效率

① 拉力 FF 做的功

已知钢缆拉力 F=1×106 NF=1×106 N，但题目说“又被匀速吊起 1 m”，这里 吊起 1 m 是指货箱上升 1 m，但拉力 FF 作用点移动的距离要看滑轮组。

没给滑轮组示意图，常见水上打捞船起重滑轮组一般是多段绳子承担货重，假设绳段数 nn，则：

s=nh物上升s=nh物上升​

题中未给 nn，但从后面“拉力 F=1×106 NF=1×106 N 时货箱完全出水后匀速上升”，可先求货箱重力：

m=200 t=2.0×105 kgm=200 t=2.0×105 kgG=mg=2.0×105×10=2.0×106 NG=mg=2.0×105×10=2.0×106 N

完全出水后，货箱只受重力 GG 与钢绳总拉力（通过滑轮组施加），匀速时：

nF=G⇒n=GF=2.0×1061.0×106=2nF=G⇒n=FG​=1.0×1062.0×106​=2

所以滑轮组绳段数 n=2n=2（动滑轮上两段绳承担货箱重量）。

那么货箱上升 h=1 mh=1 m 时，拉力 FF 作用点移动距离：

s=nh=2×1=2 ms=nh=2×1=2 m

拉力做功：

W总=F⋅s=1.0×106×2=2.0×106 JW总​=F⋅s=1.0×106×2=2.0×106 J2.0×106 J2.0×106 J​

---

② 滑轮组机械效率

有用功是提升货箱做的功：

W有=Gh=2.0×106×1=2.0×106 JW有​=Gh=2.0×106×1=2.0×106 J

总功已经求得 W总=2.0×106 JW总​=2.0×106 J。

咦？竟然 W有=W总W有​=W总​？
效率：

η=W有W总=2.0×1062.0×106=1=100%η=W总​W有​​=2.0×1062.0×106​=1=100%

这在实际中不可能，说明我的推理可能有问题：如果 n=2n=2 且 F=1×106 NF=1×106 N，那么 nF=2×106 N=GnF=2×106 N=G，确实刚好相等，额外功为 0，这不合理。

可能的情况：题目给的拉力 F=1×106 NF=1×106 N 是 钢缆上的一段绳的拉力，而滑轮组中可能这段绳 并不是直接 n=2 那样，而是更复杂的滑轮组，或者起重装置是多个滑轮组组合，题中 F 指的是最终卷扬机端的拉力。

为了求机械效率，还需要知道 nn。从“起吊装置结构示意简图”没有看到，但常见题目会隐含：若货箱完全出水后匀速上升时，拉力 FF 与货箱重力 G 符合 nF=GnF=G 则得到 nn，若 nn 不是整数就说明还有摩擦、动滑轮重等。

这里题设里没给动滑轮重，若按理想情况，则效率 100%，但显然不是。我们检查是否数据给错？
已知 G=2×106 NG=2×106 N，F=1×106 NF=1×106 N，若 n=2n=2，则 2F=2×106 N=G2F=2×106 N=G，额外功 0，效率 100%。

如果考虑现实中，动滑轮有重量，则 nF=G+G动nF=G+G动​ 会大于 GG，那就需要更多信息。

但我们看题目可能还是假设 此时钢缆拉力 F 是作用于动滑轮上的总拉力的一部分，很可能滑轮组是：动滑轮上绳子段数是 nn，每段绳的拉力是 FF，那么吊起货箱的力是 nFnF，既然匀速，有

nF=GnF=G

这是理想情况，机械效率 100%。但题目显然想让我们算效率小于 100%，那可能是已知“F 是自由端的拉力”，且 n>2，额外功来自动滑轮重。

---

那先假设：
设 nn 为承担重物的绳段数，拉力 FF 为自由端拉力（即人拉或卷扬机拉的力），总功 W总=F×s=F×(nh)W总​=F×s=F×(nh)，有用功 W有=GhW有​=Gh。

需要知道 nn 才能算。但题目没给，一个可能是从上下文“拉力 F 为 1×106 N1×106 N”和“货箱重 2×106 N2×106 N”直接看出 nF>GnF>G 还是 nF=GnF=G？

若 nF=GnF=G，则 n=2n=2 时成立，效率 100%。

若 nF>GnF>G，则 nn 应该小于 2 才可能（因为 F 固定），那 nn 只能为 1，但 n=1 就是直接吊，F 就等于 G，矛盾（因为 F=1×106F=1×106 不等于 G=2×106G=2×106）。

所以只能是 nF=GnF=G 的理想情况。

---

因此题目可能这里就是假设理想机械，效率 100%。但很多考试题会给一个动滑轮重力或额外阻力。此处未给，只能按理想算。

我们继续按理想情况算效率：

η=GhF⋅(nh)=GnFη=F⋅(nh)Gh​=nFG​

且 nF=GnF=G，所以 η=1η=1，即：

η=100%η=100%

这数值可能让出题者觉得不符合常理，但按照给定数字的确如此。

---

所以 (3) 的最终答案：

拉力 F 做功：

W总=2.0×106 JW总​=2.0×106 J

机械效率：

η=100%η=100%

（如果不按理想，则需额外数据，但题目没提供动滑轮重等信息，只能如此）

---

最终答案整理：

(1) 2.0×105 Pa2.0×105 Pa
(2) 5.0×105 N5.0×105 N
(3) 拉力做功 2.0×106 J2.0×106 J，机械效率 100%100%（按理想机械计算）。